Some recent exciting research from the IISC Bangalore has experimentally demonstrated the breakdown of the central limit theorem that the sample-sample fluctuation of N particle systems grows as N^1/2. They demonstrate that for non-equilibrium systems the fluctuation can vary as N for N particles.
Interestingly their ordering of the Copper rods only occured in the driven system (between two vibrating plates) when the rods were etched at one end, effectively making them arrow-like. Here are some of the comments from Science:
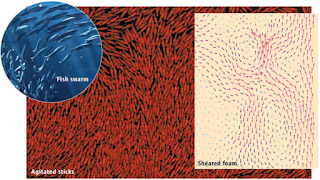
(FIGURE: Swarms and swirls. In the experiments of Narayan et al., agitated sticks form swarming states that exhibit giant number fluctuations. Similar patterns are observed in fish swarms (top left). Swirls are also observed in systems that are close to jamming, for example, in the motion of bubbles in a sheared foam (right).)
Science 6 July 2007: |
MATERIALS SCIENCE:
Shape Matters
Martin van Hecke
"Swarming and giant number fluctuations are a hallmark of the alignment displayed by driven collections of nonspherical particles. Theoretical models have been developed to describe swarming and alignment observed in schools of fish, flocks of birds, herds of sheep, or bacterial colonies--often borrowing from equilibrium models for magnetization, which consider the alignment of arrowlike objects. A very simple nonequilibrium model that exhibits cooperative motion arises when these arrows are allowed to propagate (2). In similar models, a collective response to predators and decision-making can arise (3). Toner and Tu first pointed out the giant fluctuations in such models (4).
In these systems, the particles have a preferred direction of propagation--just like real fish and birds. In 2003, Ramaswamy et al. (5) wondered what would happen for "active nematics," liquid crystals in which the particles have an orientation but have identical heads and tails (like the sticks in the present experiment). Their theory predicted that nematic systems also should exhibit giant number fluctuations, and these were recently observed in computer simulations (6).
However, when Narayan et al. tried to find such fluctuations in experiments, they encountered a surprising hurdle: cylindrical rods, arguably the simplest nematic particles, do not form nematic states and do not exhibit giant fluctuations (7). The authors achieved their present breakthrough only after etching the rods to obtain sticks with thinner ends (see the figure); for unknown reasons, these sticks exhibit nematic order. To complicate matters further, Aranson et al. recently performed similar experiments and observed that weak coupling between the nematic order and spurious in-plane vibrations of the support plate may strongly influence the swirling motion (8). Clearly, swarming is a subtle problem, and the precise nature of the swarming state and the transition to swarming is not yet fully understood.
The experiments of Narayan et al. are part of a bigger story, where nonequilibrium systems of nonspherical particles exhibit surprising behavior: We do not yet understand the consequence of shape. An earlier striking example of this is the finding that, contrary to expectation, M&M candies can be packed more effectively than spheres (9)."
REFERENCES:
- V. Narayan, S. Ramaswamy, N. Menon, Science 317, 105 (2007).
- T. Vicsek, A. Czirok, E. Ben-Jacob, I. Cohen, O. Shochet, Phys. Rev. Lett. 75, 1226 (1995).
- I. D. Couzin, J. Krause, N. R. Franks, S. A. Levin, Nature 433, 513 (2005).
- J. Toner, Y. Tu, Phys. Rev. E 58, 4828 (1998).
- S. Ramaswamy, R. A. Simha, J. Toner, Europhys. Lett. 62, 196 (2003).
- H. Chaté, F. Ginelli, R. Montagne, Phys. Rev. Lett. 96, 180602 (2006).
- V. Narayan, N. Menon, S. Ramaswamy, J. Stat. Mech. 2006, P01005 (2006).
- I. S. Aranson, D. Volfson, L. S. Tsimring, Phys. Rev. E 75, 051301 (2007).
- A. Donev et al., Science 303, 990 (2004).
- A. J. Liu, S. R. Nagel, Nature 396, 21 (1998).
- O. Dauchot, G. Marty, G. Biroli, Phys. Rev. Lett. 95, 265701 (2005).
- A. S. Keys, A. R. Abate, S. C. Glotzer, D. J. Durian, Nature Phys. 3, 260 (2007).
- W. G. Ellenbroek, E. Somfai, M. van Hecke, W. van Saarloos, Phys. Rev. Lett. 97, 258001 (2006).
- F. Lechenault, O. Dauchot, G. Biroli, J.-P. Bouchaud; available online at http://arXiv.org/abs/0706.1531v1.